As a young girl, Maryam used to make up stories in her head. In her creations, one day she’d be a leader, one day a hero, and some days she’d travel the world to fulfill her destiny. Perhaps even more remarkable was her real life. She dared to dream in a nation fresh out of war and challenged the social norms around. She saw the connections which threaded different fields of mathematics and explored the web of hyperbolic surfaces. Her research not only illuminated her own path, but opened avenues for others who came after her. She was the first woman to be awarded a Field Medal in Mathematics. We might know little of her, but every little girl in Iran knows the name.
Maryam Mirzakhani was born on 12th May 1977 in Tehran, the capital city of Iran. She had no dreams of becoming a mathematician. As a child all she wanted to do was to read all the fictional books she could find and watch TV documentaries of famous people including Marie Curie and Helen Keller. She was inspired to become a writer and from a young age had a habit of doodling. She completed her elementary school education in Tehran about the time when the Iran-Iraq war ended. She moved to a Farzanegan School for her middle school education. Farzanegan Schools were gendered schools established by Iran’s National Organization for Development of Exceptional Talents. These schools had better resources and better paid teachers. “I think I was the lucky generation”, she said, during an interview, “any older I would not have got these opportunities”.
In the same school in 6th grade she met Roya Beheshti, who would become her lifelong friend. Mirzakhani and Beheshti found a common interest to indulge in. They used to explore the bookstores near their school and buy random books off the shelves. Books during this period were very cheap and they weren’t allowed to browse or read them in stores. Beheshti says, “I remember a time when Maryam was not good at math. In the first year Maryam was the top student in every class except math”. She adds “Maryam got her test back and she got 16/20” – “Maryam was so frustrated that before putting the test in her bag, she tore it apart and said that, that was it for her. And she was not going to even try to do better. This is Maryam when she was 11. That didn’t last long, after the summer break she came back with her confidence regain and she started to do very well”. Mirzakhani’s Mathematics teacher did not think of her as a talented student, which was a blow to her confidence. At that age “it is so important what others see in you”, Mirzakhani said in an interview with Quanta.
The following year, however, Mirzakhani had a more encouraging teacher and as a result, her confidence re-emerged. Beheshti and Mirzakhani found another common interest in Mathematics after that. They both graduated to high school where they found questions to a national competition to pick candidates for International Olympiad in Informatics. They managed to solve three of the six problems over the course of several days. This gave Mirzakhani something to aspire for. They met their principal and demanded problem solving classes in mathematics comparable to the ones being taught in Boys’ school. Mirzakhani recalled her principal as being very supportive and strong, “If we really wanted something, she would make it happen”. Their principal encouraged them even though there had never been a girl on the International Team. Mirzakhani believed that the support and encouragement she received from the principal “has influenced my life quite a lot”.

Mirzakhani and Beheshti became the first women qualified for the Iranian Math Olympiad team in 1994. Mirzakhani earned a Gold medal that year scoring 41 out of 42 points, Beheshti won the Silver Medal with 35/42 points. Mirzakhani wasn’t done yet; she returned to the Olympiad the following year and achieved a perfect score and became the first Iranian to do so and earn two gold medals. Her solutions lead to her first published paper titled “Decomposition of Complete Tripartite Graphs Into 5-Cycles” in 1995 at the age of 18. So far Mirzakhani had enticed by the challenge, in her own words, “I got excited about it may be just as a challenge, but then I realized that it is really nice and I enjoy it”. Olympiads had ignited her deep love for mathematics. Mirzakhani completed her Batchelor of Science in Mathematics from Sharif University in 1999. During this she and Beheshti wrote a book titled “Elementary Number Theory, Challenging Problems”. This book they wrote when they were 22 remains a standard reference for Olympiad Training in Iran even today.
She had a sort of daring imagination. She would formulate in her mind an imaginary picture of what must be going on, then come to my office and describe it. At the end, she would turn to me and say, “Is it right?” I was always very flattered that she thought I would know.
Prof. Curtis T. McMullen
After graduation, Mirzakhani went to graduate school at Harvard University on a Scholarship. She started attending seminars by Prof. Curtis T. McMullen. A Field Medalist for his work in Complex Dynamics, Hyperbolic Geometry, and Teichmüller theory. Even though the subjects fascinated her she didn’t understand much of what was being talked about. She started going to McMullen’s office and discussing questions while scribbling notes in Farsi. “She came to my office one day, she was quite humble and unpretentious, and she began peppering me with all sorts of questions. I think I was struck by her intense curiosity and drive”, McMullen says “– I asked her to report on a paper about the phenomenon, counting the number of simple loops, on a doughnut, on a surface with one hole. And She understood this paper very thoroughly and gave a nice talk and then to my surprise she arrived in my office and said ‘well I think I have an approach to doing this for surfaces with any number of holes, 2, 3, 4, up to infinity’. Then completely on her own initiative began developing this theory of counting simple closed loop on a surface. It was very intricate and it opened up a lot of topics that are not usually thought of as related to one another”.
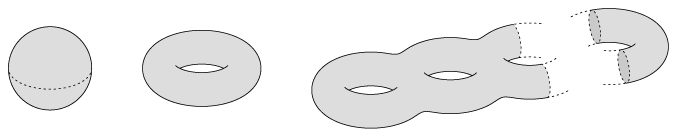
Mirzakhani became fascinated with Hyperbolic Surfaces. In ‘Real Life’ we look at things which are arranged in flat surfaces. The x-y plane and the shortest distance two points being a straight line are properties of Euclidian Geometry, wherein the curvature of space is zero. If the curvature of space is positive it is called elliptical or spherical geometry, the shortest distance between two points is never a straight line. If the curvature is negative, it is called Hyperbolic Geometry. Every point of this geometry is curved like a saddle. Any surface eventually forming in on itself. We can classify surfaces into classes based on the number of holes in them which are called ‘genus’. A sphere has genus 0, a doughnut has genus 1, and a pretzel has genus 2, and so on. Hyperbolic geometry is famously difficult to do visualize or even imagine. Mirzakhani however had an over-abundance of imagination; she could not just understand but also form analogies and visualize the shapes and structures like characters from a story.
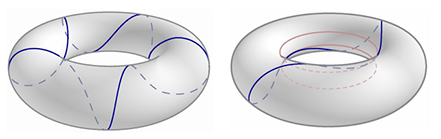
The ‘closed loops’ on surfaces that Mirzakhani Studied are called `Closed Geodesics`. Geodesics are simply the ‘straight lines’ of curved space which join two points along the shortest distance. Imagine a surface like a sphere, if you start drawing a straight line from any point, it will eventually close back on itself, this is called a ‘Closed Geodesic’. A sphere or surface with genus 0 is easier because doesn’t matter where you start, you will always end up at the same point forming a circle. Now imagine a genus 1 surface, a doughnut, it is harder to start cutting it in a straight line so that you reach the exact point again, slight deviation when you start could lead you in a spiral. Now imagine a shape like the letter eight or symbol for infinity, it is even harder. Additionally, most of the closed geodesics of this shape would intersect with themselves. Some however would not, these are called `Simple geodesics`. These Simple Geodesics are important because they can be studied to define and study the entire surface. One of the most important questions during Mirzakhani’s time was ‘How many simple closed geodesics of a specified length can a surface have’.
The majority of mathematicians will never produce something as good — “and that’s what she did in her thesis.
Benson Farb
Mirzakhani’s doctorate thesis in 2004 under Prof. McMullen answered this question. Which he explained rather proudly, during her Field Medal ceremony. “This will be my first result of Mirzakhani that I would like to discuss. So, the problem is, count the number of simple loops on a fixed Riemann surface of a length less than equal to L. Most loops on a Reimann Surface cross each other. It is very hard for a loop on a Reimann Surface to not cross itself. By Investigating this very natural and naïve question about one Reimann Surface, Maryam was led to a cascade of unexpected new results. First, she gave new proof of the Witten Conjecture. Proof and intuition of it was String theory, and what Mirzakhani was able to do was show that this formula flows forth naturally”. Mirzakhani’s work was important on its own but she was also able to weave in this into other major research questions. One of them was a Witten Conjecture in Mathematics of String theory, and another was concerning the volume of “Moduli” space. She also gave very crucial statistics of such surfaces depending on their genus.
It was her ability to see these connections that made Mirzakhani’s work so special. It is atypical for a research fellow to make such an impact with their doctoral thesis. Solving each of these problems would have been consequential on their own, Mirzakhani did both and also found the connections between them. She published her thesis in three papers in top journals of Mathematics.
Jan Vondrak, recalled a run with his future wife Maryam, “She’s very petite, and I was in good shape, so I thought I’d do well, and at first, I was ahead”, “But she never slows down. After half an hour, I was done, but she was still running at the same pace”. Mirzakhani had similar approach to her work, she was a self-proclaimed ‘slow mathematician’. She liked to chew on her problems for months or years and eventually produce results which were more elegant than anyone expected. Her work, almost always involved doodling, a habit she had from her childhood. “She has these huge pieces of paper on the floor and spends hours and hours drawing what look to me like the same picture over and over”, Vondrak said. During an interview, Mirzakhani said “the process of drawing something helps you somehow to stay connected”. Mirzakhani and Vondrak’s daughter Anahita, used to exclaim, “Oh, Mommy is painting again!” when Maryam was working.
In 2006 Maryam was working on the problem of hyperbolic surfaces when its geometry is deformed. Imagine twisting the letter 8 from the middle. Before her work, “this problem was completely unapproachable”, McMullen said. She compared this mechanism of deforming shapes with a type of earthquake. “With a one-line proof”, McMullen said, “she constructed a bridge between this completely opaque theory and another theory that’s completely transparent”. “It illustrates a kind of thinking that I think is very novel and is very characteristic of Mirzakhani’s research. Namely, I have been discussing Moduli spaces as if it has these two different personalities that are battling for control. What Mirzakhani did to prove this result is she found a bridge between these two sides. And then you can take whatever somebody has proven on one side of the bridge and carry it to the other side and call it your own theorem. So that’s the kind of thinking that I think just was completely unexpected and is bound to lead to many new results and many new ways of looking at Moduli Spaces”.
– most of the time, doing mathematics for me is like being on a long hike with no trail and no end in sight.
Maryam began working with ‘one of her favourite collaborators’, Alex Eskin in 2006. He recalls “She is very optimistic, and that’s infectious”, he said. “When you work with her, you feel you have a much better chance of solving problems that at first seem hopeless”. After doing a few projects together, they decided to work on the ‘Billiards Problem’. “If you have a Billiards table and you start from a point and hit the ball and it hits the boundaries and it moves say forever. You want to see the trajectory of the ball. Would it cover all your billiard table? Can you find closed billiard paths? Interestingly enough this is an open question in general, if you don’t place any restrictions on the angles of the polygon that you started (with)”. Billiards provides some of the simplest examples of dynamical systems. Dynamical systems are systems that evolve over time according to a given set of rules. The behaviour of the ball has proven unexpectedly hard to pin down. “Rational billiards got started a century ago, when some physicists were sitting around saying, ‘Let’s understand a billiard ball bouncing in a triangle” said Alex Wright, a researcher at Stanford. “they thought they would be done in a week, but 100 years later, we’re still thinking about it.”
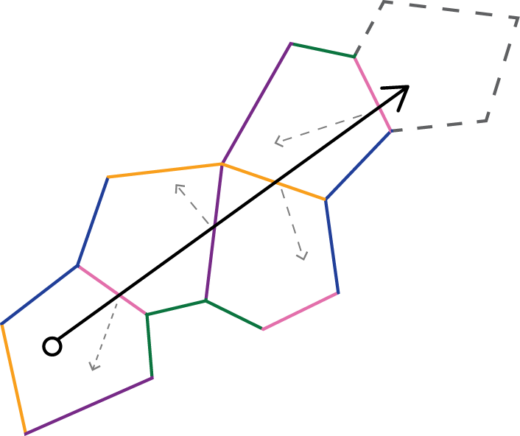
Imagine a Billiards table, if a ball moving is bounced off a side, it would do so in a specific angle. If you imagine placing a mirror at this side, you’d see the reflection of the ball continuing in the same direction in the mirror table. You can therefore keep extending these mirror tables and the ball would keep moving in the same direction. If you end up with a table oriented in the same way as the original table, you can assume that the ball’s path is a loop. If you glue together these mirrors in a hyperbolic space you will end up with a surface of genus 2. Before Mirzakhani, McMullen, her advisor had famously provided calculations and results on this problem. His research was hailed as a huge advance in the field. Although even before he had published, Maryam, still a graduate student, had approached him and asked “Why did you just do genus two?”. “That’s the kind of person she is,” he said. “What she sees hints of, she wants to understand more clearly.”
After five years of slow and tedious work, in 2013, Mirzakhani and Eskin succeeded in generalising McMullen’s results to all surfaces of genus more than two. It was Mirzakhani’s optimism and tenacity that kept the pair going, Eskin said. “Sometimes there were setbacks, but she never panicked”, he said. Their work has been hailed as a massive improvement in the tools available to study Moduli spaces. “It’s as if we were trying to log a redwood forest with a hatchet before, but now they’ve invented a chain saw”, Alex Wright said. Mirzakhani herself was amazed that they didn’t give up, “If we knew things would be so complicated, I think we would have given up”, she said. “I don’t know; actually, I don’t know. I don’t give up easily”.

In 2014, Maryam Mirzakhani became the first woman, and the first Iranian, to be awarded a Fields Medal in Mathematics. Which is considered the Nobel Prize of Mathematics. “Maryam never liked to brag or even talk about her achievements”, said Beheshti. Maryam when asked about her contributions once said, “To be honest, I don’t think I’ve had a very huge contribution”. When she received the email regarding her winning the Fields Medal, she assumed that the account from which the email was sent had been hacked. She didn’t want to be the ‘Face or women in Mathematics’, she much rather wanted to focus on her research. “There are really many great female mathematicians doing great things”, she said. Newspapers in Iran and some worldwide, ran old photos of her with a Hijab on or edited her images to add a scarf on her.

In 2013, an year before her medal, she was diagnosed with Breast Cancer. She started treatments and was gradually getting better. She didn’t want to slow down and started planning a collaboration with Alex Wright regarding a “Magic Wand” for understanding Billiards and Translation Surfaces. In 2016, her cancer reappeared had spread to her bones and liver. Maryam gave her health the priority and started spending more time with her family. However, she didn’t stop carrying out her responsibilities. She still taught classes, graded papers, and guided students. While her parents were in Iran and could not get a visa to visit her because of a blanket ban by the USA, her husband and her sister were with her. Her parents could finally meet her in her last months. In 2017, at the age of 40, she passed away. The nation mourned, and its president tweeted a photo of her without a Hijab on to break taboo. She was the first woman since 1976 whose photo was published in Iranian newspapers without a scarf.
“It was a difficult time, but still when it came to anything related to math it was uplifting and inspiring to talk to her. She had such a positive personality, it really always felt good to talk to her”. She one said, “You have to ignore low-hanging fruit, which is a little tricky”, “I’m not sure if it’s the best way of doing things, actually — you’re torturing yourself along the way”. She always wanted to be a writer, so she wrote a story that continues to inspire young women in Iran and world over. This is the story of Maryam Mirzakhani.
Sources:
- https://www.quantamagazine.org/maryam-mirzakhani-is-first-woman-fields-medalist-20140812/
- http://nrs.harvard.edu/urn-3:HUL.InstRepos:34310044
- http://chalkdustmagazine.com/features/mathematics-maryam-mirzakhani/
- https://dash.harvard.edu/bitstream/handle/1/34310044/icm14.pdf
- https://news.stanford.edu/press-releases/2017/07/15/maryam-mirzakhanedal-winner-dies/
- https://www.zoomit.ir/2017/7/15/189155/maryam-mirzakhani-biography/
- https://www.quantamagazine.org/maryam-mirzakhani-is-first-woman-fields-medalist-20140812/
- https://news.stanford.edu/press-releases/2017/07/15/maryam-mirzakhanedal-winner-dies/
- https://www.zoomit.ir/2017/7/15/189155/maryam-mirzakhani-biography/
- https://www.wired.com/2014/08/maryam-mirzakhani-fields-medal/
- https://www.bbc.com/persian/science/2014/08/140813_l45_maryam_mirzakhani_math_medal
- https://kknews.cc/health/a8rbglv.html
Clips:
- https://www.youtube.com/watch?v=Sx-kAlEpiZk
- https://www.youtube.com/watch?v=4GhbMhQLQ_g
- https://www.youtube.com/watch?v=8Nl8drJyeDc
- https://www.youtube.com/watch?v=ffh4Oe-k-kQ
- https://www.youtube.com/watch?v=HUBnzTTQ5jk
- https://www.youtube.com/watch?v=VC7MZv1JH8w
